Material science for photonics
During the initial stages of my research career, I focused on the material science aspects of photonics. I studied my PhD at the Material Science Institute in Madrid (CISC) under the supervision of Prof. C. López where I worked to the fabrication of three-dimensional self-assembled structures and their interaction with light. From self-assembled ordered photonic crystals to completely disordered structures, called photonic glasses (see Figure 1b and c, respectively). The overall aim of my PhD thesis was to exploit the interplay between order and disorder to control the transport of light.
Fig. 1. Self-assembled photonic structures 
(a) Picture of a self-assembled photonic crystal (left) showing visible iridescences due to Bragg reflection and a photonic glass (right). (b) and (c) are scanning electron micrographs (SEM) of these two structures, respectively. (d), (e) and (g) are SEM pictures of ZnO photonic crystals obtained by chemical vapor deposition using self-assembled photonic crystals like the one shown in (b) as templates. (f) Using the same technique, we can obtain ZnO photonic glasses.
From Sanskrit upala (gemstone), an opal is a self-assembled face centered cubic (fcc) arrangement of monodisperse dielectric microspheres (see Fig. 1b). Natural opals are composed by SiO2 microspheres and show bright visible iridescences due to Bragg reflections from crystallographic planes of the structure as shown in Fig. 1a. Such a structure acts, therefore, as a three dimensional photonic crystal for visible light (with wavelength comparable to the diameter of the spheres) with very high quality features. The monodispersity of the spheres defines the minimum free energy configuration to be the fcc structure and, among the possible fabrication methods used to obtain them, self-assembling gives rise to the best quality samples. By mimicking nature, it is possible to grow artificial opals with polymeric microspheres such as polystyrene or polymethyl-methacrylate. To date, these are the only scalable three-dimensional photonic crystals with remarkable optical properties. I used these polymeric structures as templates to fabricate more advanced structures employing inorganic materials such as ZnO. During my PhD, I made use of a controlled metal-organic chemical vapor deposition process to fabricate large-area of high-quality ZnO templates with fine control over the filling volume [Adv. Mater. 17, 2761 (2005)]. Figure 1 d, e and g show SEM pictures of this ZnO nanostructure. A remarkable property of ZnO relies on its strong excitonic UV photoluminescence at room temperature. This photoluminescence can be enhanced even further by nanostructuring the material. By doing so, I could obtain UV lasing out of these self-assembled structures [J. of Mater. Chem. C 1 (44), 7357 (2013)]. The physical mechanism under this lasing emission relies on the interplay between the periodic structure and the gain material. Nanostructuring a gain material like ZnO simultaneously creates a feedback mechanism due to interference with the nanostructure while, at the same time, enhances the light-matter interaction improving the gain efficiency and minimizing the lasing threshold. Light propagating through such a structure presents an extraordinary low group velocity which provides the necessary feedback for light amplification leading to a distinct lasing threshold behavior as observed while increasing the excitation power.
Fig. 2. Resonant diffusion through photonic glasses 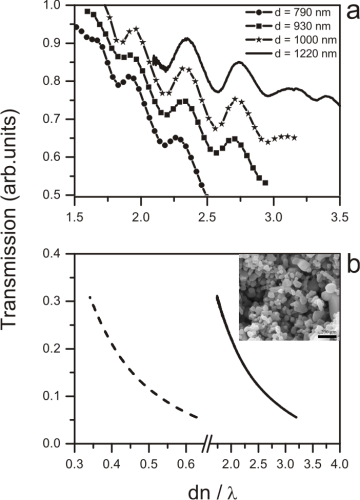
a) Normalized total transmission of white light through photonic glasses as a function of the sphere diameter scaled to the wavelength of light and the refractive index. Samples are composed of spheres with four different diameters and the thickness is about 100 μm in all cases. b) Total transmission of white light through two different reference samples as a function of the scaled diameter. The dashed line represents total transmission through photonic glasses made of PS spheres with d = 200 nm. The solid-line represents total transmission through a powder made of TiO2 with averaged d = 850nm (the inset is a scanning electron micrograph of the sample with the scale bar representing 200nm). Figure taken from [Adv. Matter. 22, 12 (2020)].
Another important direction of my PhD was to obtain completely random self-assembled structures that we called photonic glasses (see Fig. 1(c)) as opposed to photonic crystals. The most remarkable property of photonic glasses is that it allows resonant light diffusion when light propagates through these structures. Light propagation through a homogenous medium as air or a glass slab is ballistic, that is, the propagation direction remains fixed during the process. If scattering particles are added to a homogenous film, the light propagation direction becomes increasingly randomized and when light travels through a very disordered system such as white paint, it is multiply scattered and ballistic propagation can no longer describe the transport process. Then, the transport process is diffusive and interference effects can be ignored to a first approximation. Processes described by diffusion are ubiquitous in nature: from molecules under a pressure gradient to (matter, electromagnetic, sound or seismic) waves in random systems.
The peculiar optical properties of photonic glasses are due to the light-scattering response of the dielectric spheres of which they are composed (see Fig. 1c). A single dielectric microsphere with size comparable to the wavelength of light (a so-called Mie sphere), can sustain electromagnetic resonances. When all the spheres are identical (within 2% fluctuations in our case), these modes occur all at the same frequency. In a photonic glass, the diffusion of light is therefore strongly affected by the behavior of the individual spheres and it is possible to observe resonances in the light transport (Fig. 2a) as opposed to the monotonic response of a standard random material (Fig. 2b) where all the components are different in size or shape. By means of independent static and dynamic measurements, we measured the resonances in the transport mean free path, the diffusion constant and, also, the energy velocity of light. We demonstrated a diffusive resonant material for the first time [Phys. Rev. Lett. 99, 233902 (2007)]. This novel material joins light dispersion and diffusion in the same system, a combination that can be crucial to control the diffuse flow of light in analogy to what photonic crystals do for ballistic light.
Figure 3. Photonic crystals with controlled disorder 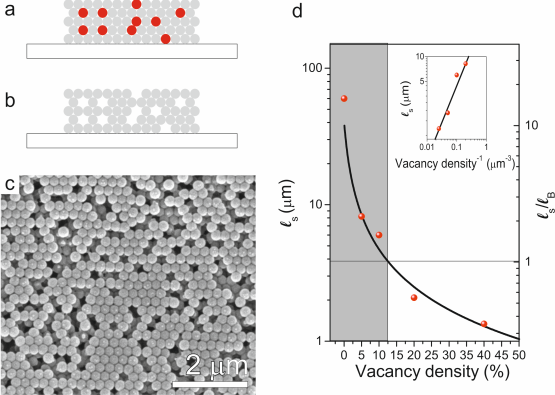
(a) The diagram schematizes the film growth by vertical deposition when polystyrene spheres (PS, red) and polymethyl-methacrylate spheres (PMMA, gray) are mixed together in the initial colloidal suspension with different diameters. The structure that forms depends on the diameter ratio of the spheres and is generally random. By etching with cyclohexane the PS spheres can be removed (b). In (c) a SEM image is shown of such structure. (d) The scattering mean free path is plotted vs vacancy density and compared to the Bragg length (lB, shaded area) in the case of ρv = 0%. The black dashed curve represents the fit of ls vs ρv. Images taken from [Phys. Rev. A 84, 023813 (2011)] and [J. of Mater. Chem. C 1 (44), 7357 (2013)].
In the final stage of my PhD, I explored the intermediate scenario between photonic crystals and glasses, which is a partially ordered and disordered structure. Photonic crystals are extremely sensitive to structural disorder even to the point of completely losing their functionalities. While, on one side, this can be detrimental for applications in traditional optical devices, on the other side, it gives also rise to very interesting new physics and maybe even new applications. We propose a route to introduce disorder in photonic crystals in a controlled way by creating a certain percentage of vacancies in the lattice (see Fig. 3a-c). An alloy photonic crystal is grown with a binary colloid that consists of spheres of two types. If both type of spheres are chemically different but of the same diameter, it is possible to also obtain a regular lattice of which, after crystal growth, one of the constituents can be chemically removed. In our case, we used binary colloidal suspensions of polymethyl-methacrylate (PMMA) and polystyrene (PS) spheres. This method allows us to grow large homogenous three-dimensional alloys with fcc crystalline structure and appreciable thickness. While the growth process fixes the crystalline structure, with this method we introduce disorder without altering the particular crystalline structure, by adding a controlled amount of vacancies in the lattice. Once the alloy colloidal crystal is grown, the PS spheres are removed by selective chemical etching by immersing the alloy in a selective etching that only solves the PS spheres. This procedure completely removes the PS spheres, leaving the PMMA spheres undisturbed. We use this system to probe the role of disorder on the resulting transport properties from various points of view, including measurements of the transport and scattering mean free path (see Fig. 3d) and the diffusion constant [Physical Review B 79, 241109(R) (2009)] and [Physical Review A 84, 023813 (2011)]. The novelty here is the possibility to effectively tune the disorder parameter in three-dimensional photonic crystals which allow us to probe the optical properties of structures in between order and disorder. By doing so, we are able to study how the controlled introduction of disorder progressively destroys the periodic backbone thus engineering the number of scattering events light suffers across an actual sample of any given thickness and tuning the scattering parameters as the mean free path and the diffusion constant.
When the amount of vacancies is sufficiently high (typically around 40% of the total lattice sites), these structures show the same optical resonances as those of a photonic glass composed of spheres with the same diameter. The scattering mean free path, ls, which is the average distance between two scattering events, is a very good parameter to characterize the degree of disorder of a structure. The shorter the mean free path, the larger the degree of disorder. Fig. 3d shows how it varies when adding vacancies at random positions in absolute units and in units of the Bragg length of the unperturbed crystal, lB. The Bragg length is the attenuation length in the photonic-crystal band gap due to Bragg interference. For low vacancy density, ls » lB, random multiple scattering due to imperfections in the crystal can be considered negligible. However, when the density of vacancies increases up to 20%, the scattering mean free path becomes smaller than the Bragg length, ls < lB. In that case, random multiple scattering prevails and classical diffusion explains light propagation in the structure much more accurately. Adding vacancies in a controlled way to a self-assembled opal is, therefore, a way to tune the amount of random multiple scattering in a photonic crystal and implies a transition from a crystal to a glass without altering the lattice. This has consequences in the nature or the lasing emission when a gain optical material is added to the structure: we observed a transition between lasing in the ordered structure (Bloch lasing) to lasing in the disordered structure (random lasing) [J. of Mater. Chem. C 1 (44), 7357 (2013)].
