Complex optomechanics

After many years exploring the role of disorder and imperfection in systems used in quantum photonics, I turned my attention to the field of optomechanics. The systems and nanostructures used in quantum photonics are sufficiently small to be very sensitive to thermal energy. At room temperature, thermal energy activates vibrations around frequencies from the 100’s of MHz to few GHz. In general, phonons and vibrations are very detrimental for quantum photonics as the solid-state emitters used suffer from lattice vibrations and the photons emitted become distinguishable. Beyond that obvious reason to study phonons in these systems, my interest has been to explore the role of imperfection in the optomechanical coupling, the coupling between light at telecom wavelengths and the mentioned vibrations.

Fig. 1. Optomechanics in complex systems

Nonlinear dynamics in disordered optomechanical systems

I have studied complex phononic systems where the modes with frequencies within the GHz range are excited thermally at room temperature so no external excitation scheme is required. Here, we explore disorder to mediate the interaction between GHz vibrations and THz photons. These systems exhibit remarkably rich nonlinear dynamics that emerge from the interplay between optical and mechanical degrees of freedom. When operating at high optical powers, silicon-based optomechanical cavities display strong nonlinear behavior dominated by two-photon absorption (TPA), free-carrier dispersion (FCD), and thermo-optic (TO) effects. The competition between free-carrier-induced blueshifts and temperature-induced redshifts of the optical resonance can drive the system into self-pulsing regimes, where the cavity field oscillates periodically even under continuous-wave excitation. This self-pulsing phenomenon represents a limit cycle in the phase space defined by carrier density and temperature, and can itself drive mechanical oscillations through radiation pressure modulation. We also exploit silicon material nonlinearities to modulate the optical modes in these systems. The strongly-driven nonlinear optical response creates periodic modulation of the intracavity field, which in turn generates time-varying radiation pressure forces on the mechanical resonator. This coupling mechanism enables mechanical amplification and self-sustained phonon lasing even in the presence of disorder-induced losses.

Disorder as a resource in optomechanics

Any photonic or optomechanical nanostructure is affected by some degree of imperfection. This is due to the unavoidable finite tolerance of the fabrication process. In this line of research, we investigate the role and limitations imposed by disorder for the photon-phonon interaction. We also explore novel ways of exploiting disorder as a resource to enhance this coupling in complex systems.

Fig. 2. Shamrock optomechanical crystals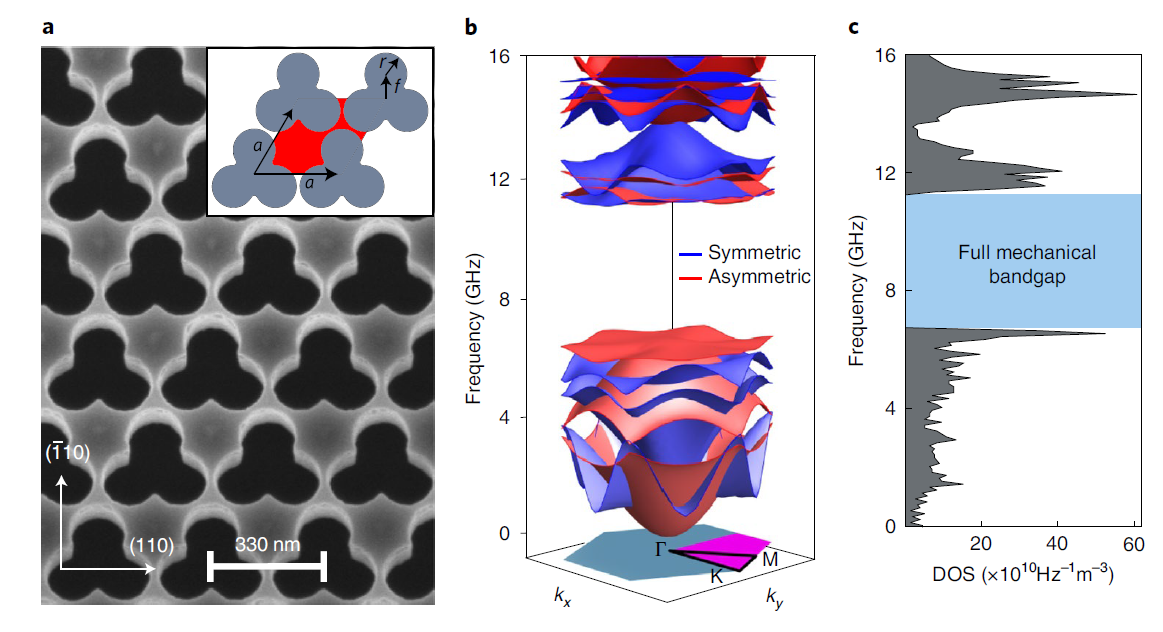

We have explored Anderson-localized cavity optomechanics in a two-dimensional optomechanical platform: a waveguide etched in a suspended silicon membrane that incorporates a slotted line air defect. Inherent and unavoidable fabrication imperfections are adequate to induce sufficient backscattering to realize Anderson localization of optical modes. The introduction of an air slot allows for a strong confinement of the electromagnetic field that is guided along the slot, and enhances the ability for light to couple to in-plane mechanical motion.

The resulting tightly confined Anderson-localized modes can be driven to enable mechanical amplification and self-sustained phonon lasing via optomechanical back-action. The rich nonlinear dynamics of these systems manifest in multiple ways: through dynamical backaction that modifies the mechanical damping rate, through self-pulsing-driven mechanical oscillations, and through the complex interplay between multiple competing nonlinear mechanisms operating at different timescales. We design the photonic and phononic band structures to realize mechanical lasing up to 6.8 GHz that results from confinement of the mechanical mode. We confirm the existence of this mode through a combination of cavity optomechanical techniques and Brillouin light scattering spectroscopy. The role of disorder in cavity optomechanics has thus far been largely overlooked but our results show that disorder plays a crucial role, which in part can have a decisive impact on device functionality and in part opens perspectives for studies of multiple scattering and Anderson localization of bosonic excitations with parametric coupling to mechanical degrees of freedom

Related work

This research line has been extensively developed through two PhD theses I supervised:

Light-motion interaction in disordered nanostructures
Guillermo Arregui Bravo (2021)

This thesis provides comprehensive theoretical and experimental analysis of optomechanical interactions in disorder-induced cavities. It includes detailed treatment of the nonlinear dynamics arising from two-photon absorption, free-carrier dispersion, and thermo-optic effects in silicon cavities. The work demonstrates self-pulsing phenomena in Anderson-localized optical modes and shows how these limit cycles can drive mechanical oscillations through radiation pressure modulation. The thesis also presents the statistical enhancement of optomechanical coupling rates in Anderson-localized systems and demonstrates mechanical lasing up to 6.8 GHz in slotted photonic crystal waveguides.

Brillouin scattering in bosonic systems
Omar Enrique Florez Peñaloza (2023)

This thesis focuses on the design and experimental characterization of phononic crystals and waveguides using Brillouin light scattering spectroscopy. It demonstrates full hypersonic bandgaps with up to 64% gap-to-midgap ratio in shamrock phononic crystals and provides direct experimental evidence of guided modes at GHz frequencies measured at room temperature. The work explores both trivial defect waveguides and topological waveguides based on quantum spin Hall and quantum valley Hall analogies, addressing the design constraints related to material anisotropy and experimental characterization.

I summarize most of the results of this research line in this talk.